どこへもだどりつけない

しばらく前だが、乱歩の問題あるいは酔歩の問題というのを知って例をいくつか作った。その一つ。

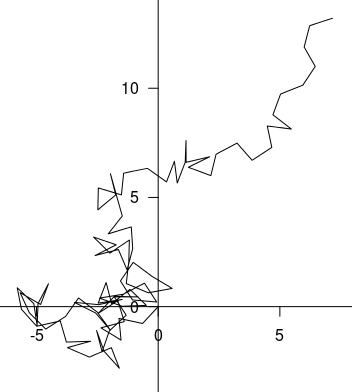
原点から出発した酔っぱらいが、左下の領域から左上、さらに右上へさまよって行く。終点は100歩目である。

こいつはもう出発点にもどることはできない――というのが直感だったが、考えてみれば、100歩どころか最初の一歩を踏み出した時点で出発点にもどることはもうできないのではないか。というのも、乱歩、酔歩、あるいはランダムウォークとも言うのだが、出発点からランダムに選んだ方向に歩き出した酔っぱらいが、次のランダムな選択でぴったり逆方向に向かうことはできるのか。ほとんどできないのではないか。ただ、その「ほとんど」は全くのゼロなのか、それともゼロに近いが確率としてはありうるのか。

それ以上考えは進まなくて忘れていたのだが、今朝こんな記事にぶつかった。
- The Adventures of Dr.Hara: ルイス・キャロルと無限小の確率

これによると、自分が考えかけたような問題は現代数学ではけりがついているという。あてもなく歩き出した酔っぱらいが出発点にもどれる確率は、最初の一歩にしてすでにゼロである。

Choo Choo Train 誰もぼくを
見つけられないほど遠くへ oh oh
片道切符にぎって
たどりつけないどこへも

- 田島貴男版「恋の片道切符」