天球の大きさのこと
天文学でいう天球は、生物学者のヤーコプ・フォン・ユクスキュル(1864-1944)がいう最遠平面(fernste Ebene)にあたる。一方は「球」、他方は「平面」だが、同じものである。
観測者から最遠平面までの距離が 20m ということは、天球の半径がわずか 20m というのと同じ。しかもその距離は体調によって変わるらしい。どういうことか。
ユクスキュルがあげる別の例。生理学者・物理学者のヘルマン・フォン・ヘルムホルツ(1821-1894)の場合。
幼いころのヘルムホルツがポツダムの陸軍教会のそばを通りかかったときのこと。
教会の回廊にいる数人の労働者に気づいた彼は、
「あの人形を取って」
と母親にせがんだ。労働者の姿が彼の最遠平面上にあったため、遠く離れたところにいる人間としてではなく、小さな人間として彼には見えたのだった。
ユクスキュルによると、人間は周囲 10m 以内にある物体については目のレンズを筋肉で調節して遠近を判断できる。乳児の場合はこの距離に最遠平面があり、それより遠くにあるものについては遠近感を失い、大小としてしか判断できない。経験をかさねることで最遠平面は遠くへひろがり、おとなでは 6km から 8km の距離となる。
最遠平面は動物種によっても異なる。
ユクスキュルの観察では、イエバエの視界(最遠平面への距離)は 50cm ほど。
ヒトやイエバエだけでなく、視覚を持つすべての生物はそれぞれの最遠平面にかこまれて、言いかえればそれぞれの半径のシャボン玉の内側で暮らしている。
ユクスキュルは、それぞれの生物種やそれぞれの個体によって異なる最遠平面すなわち天球があるとし、その半径を人間のおとなの場合は 6km から 8km としたが、天文学の側からも(というより、初歩的な幾何によって)、以下のように半径の見当をつけることができる。
次の図で、円の部分は地球の断面。その中心を C とし、R を半径とする。
O は地上に立つ観測者の目の位置、h は地面からの高さ。
この場合、理論的には OHが天文学でいう地平線だが、現実の観測者の視線は下方にずれて OH' の方向となる。このうち観測者の視界に入るのは OB の部分で、B から先は地球(の地面や海面)にさえぎられて視界から外れる。
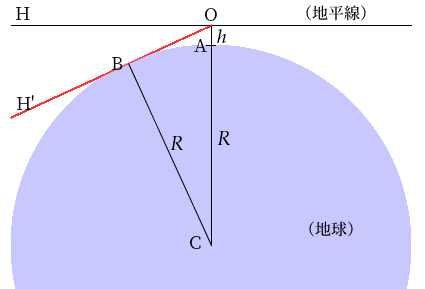
OB の長さは √(2Rh) で近似でき、観測者の目の位置 h を 1.6m から 1.8m として計算すると、OB は 4.5km から 4.8km となる。天球は観測者の目に入るものがすべて収まるサイズでなければならないから、その半径は OB より大きく、おおざっぱに言って 5km 以上となる。B 地点の付近に高い建物や山があったり、飛行機が飛んでいたりすれば、天球はこれらも容れるものとして認識されるから、B 地点の物体は天球の半径を押し広げる。
おとなの最遠平面の半径を 6km から 8km とする根拠をユクスキュルは示していないが、この値は上の計算で出した 5km 以上という値と矛盾しない。というより、ごくごく大ざっぱには一致する。
天球の半径を 5km あまりとして上の図に書き加えると、次のようになる。
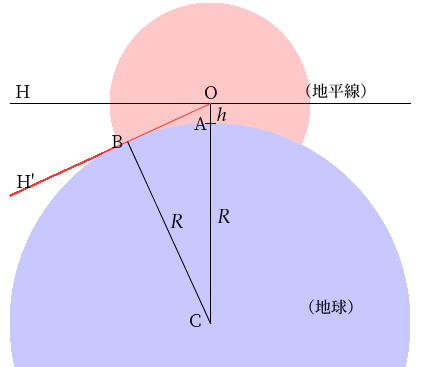
この図で、人間の目の高さ h は地球半径の10分の1の大きさで描かれている。これを実比率で描くと、天球は A の地点にあって、大きさは芥子粒ほどにもならない。論理的には地球をその内部におさめた巨大な球である天球を、地表にちょこんと載った小球のスケールでわれわれはながめている。
太陽と月と星は、見えるものすべてを取り囲んでいる同一の最遠平面上を、たがいに奥行きの隔たりなしに移動している。その最遠平面の位置は固定されていて動かないというわけではない。私が重いチフスにかかった後はじめて外に出たときには、二〇メートルほど先に色つきの壁紙のように、最遠平面が下がっていて、その上に目に見えるものすべてが描かれていた。二〇メートルより向こうには遠いものも近いものもなく、小さなものと大きなものがあるだけだった。私のかたわらを通り過ぎる車までがその最遠平面に到達するやいなや、それ以上遠ざかるのではなく、ただ小さくなっていくのだった。 ――ユクスキュル『生物から見た世界』(日高敏隆、羽田節子訳)
観測者から最遠平面までの距離が 20m ということは、天球の半径がわずか 20m というのと同じ。しかもその距離は体調によって変わるらしい。どういうことか。
ユクスキュルがあげる別の例。生理学者・物理学者のヘルマン・フォン・ヘルムホルツ(1821-1894)の場合。
幼いころのヘルムホルツがポツダムの陸軍教会のそばを通りかかったときのこと。
教会の回廊にいる数人の労働者に気づいた彼は、
「あの人形を取って」
と母親にせがんだ。労働者の姿が彼の最遠平面上にあったため、遠く離れたところにいる人間としてではなく、小さな人間として彼には見えたのだった。
ユクスキュルによると、人間は周囲 10m 以内にある物体については目のレンズを筋肉で調節して遠近を判断できる。乳児の場合はこの距離に最遠平面があり、それより遠くにあるものについては遠近感を失い、大小としてしか判断できない。経験をかさねることで最遠平面は遠くへひろがり、おとなでは 6km から 8km の距離となる。
最遠平面は動物種によっても異なる。
ユクスキュルの観察では、イエバエの視界(最遠平面への距離)は 50cm ほど。
ヒトやイエバエだけでなく、視覚を持つすべての生物はそれぞれの最遠平面にかこまれて、言いかえればそれぞれの半径のシャボン玉の内側で暮らしている。
ユクスキュルは、それぞれの生物種やそれぞれの個体によって異なる最遠平面すなわち天球があるとし、その半径を人間のおとなの場合は 6km から 8km としたが、天文学の側からも(というより、初歩的な幾何によって)、以下のように半径の見当をつけることができる。
次の図で、円の部分は地球の断面。その中心を C とし、R を半径とする。
O は地上に立つ観測者の目の位置、h は地面からの高さ。
この場合、理論的には OHが天文学でいう地平線だが、現実の観測者の視線は下方にずれて OH' の方向となる。このうち観測者の視界に入るのは OB の部分で、B から先は地球(の地面や海面)にさえぎられて視界から外れる。

OB の長さは √(2Rh) で近似でき、観測者の目の位置 h を 1.6m から 1.8m として計算すると、OB は 4.5km から 4.8km となる。天球は観測者の目に入るものがすべて収まるサイズでなければならないから、その半径は OB より大きく、おおざっぱに言って 5km 以上となる。B 地点の付近に高い建物や山があったり、飛行機が飛んでいたりすれば、天球はこれらも容れるものとして認識されるから、B 地点の物体は天球の半径を押し広げる。
おとなの最遠平面の半径を 6km から 8km とする根拠をユクスキュルは示していないが、この値は上の計算で出した 5km 以上という値と矛盾しない。というより、ごくごく大ざっぱには一致する。
天球の半径を 5km あまりとして上の図に書き加えると、次のようになる。

この図で、人間の目の高さ h は地球半径の10分の1の大きさで描かれている。これを実比率で描くと、天球は A の地点にあって、大きさは芥子粒ほどにもならない。論理的には地球をその内部におさめた巨大な球である天球を、地表にちょこんと載った小球のスケールでわれわれはながめている。