輪郭は実在しない
地平線、水平線は、存在するのかしないのか(⇒関連記事)。
それらは実在はしないが、仮想的には存在して、観察者個人を基準にすれば、かつその限りにおいて、その所在を言うこともできる。
同様のものとして、ほかに何があるか。
虹は実在するか。
虹は雨粒や霧などの集まりに太陽などの光が当たって生まれる現象だから、水滴という実体がある。実体があれば触ることはできる。さわれるものは実在するといっていいい。
観察者が虹に近づいても、虹は虹のままでいるのか。それとも虹ではなくなってしまうのか。仮に虹としては消えてしまっても、水滴として実体が残っていれば、それは実在するといえるのではないか。当該観察者の目からは消えても、おおかたの観察者にとっては依然として虹に見えているのであり、かつ実体としても存在する。
すなわち、虹は実在する。
実在するものは、客観的な座標系のもとで所在を定めることができる。
山の稜線は実在するか。
理想化されたものとして考えると、稜線には幅がない。質量もない。それでも実在するといえるか。
実在するといえる。稜線は目で見ることができ、現地に行けばその上を歩くことができ、手で触れることもできる。視覚と触覚の両方で認識できるものは、実在するといえる。
適当な座標系があれば(この場合は地図で使われる地理情報になるだろうが)、稜線の座標は決まる。
では、次図の円柱はどうか。
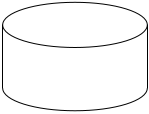
円柱の上面と下面を縁取る円周は実在するか。
この図で円周は実線で描かれているが、現実の円柱には通常そのような線は描かれていない。けれども、円周は円柱の上面と側面を分ける境界として観察者から視認でき、また触れることもできる。すなわち、この円周は山の稜線と本質的に同じものであり、それゆえ実在するといえる。
問題となるのは図の直線部分。
この二本の縦線も円周と同じように実線で描かれているが、これらの線も現実の円柱の一部ではない。
二本の縦線によって示される部位は、円柱と円柱でないもの(円柱の外側)を分ける境目として観察者には見えている。けれども、さわって確かめることはできない。円柱の側面全体に触れることはできても、そこがいま現にわたしの見ている円柱と円柱でないものの境目であるという指標、たとえば突起や溝を、指先で確認できるわけではない。
ただし水平線・地平線と同様、観察者本人を基準とした場合のみ、この縦線の座標を言うことができる。
観察者本人の視野にだけ存在し、触覚で確かめることができない点で、問題の円柱の部位は地平線・水平線の同類である。
これを一般化すると、「輪郭は実在しない」ということが一つの結論として得られる。
それらは実在はしないが、仮想的には存在して、観察者個人を基準にすれば、かつその限りにおいて、その所在を言うこともできる。
同様のものとして、ほかに何があるか。
虹は実在するか。
虹は雨粒や霧などの集まりに太陽などの光が当たって生まれる現象だから、水滴という実体がある。実体があれば触ることはできる。さわれるものは実在するといっていいい。
観察者が虹に近づいても、虹は虹のままでいるのか。それとも虹ではなくなってしまうのか。仮に虹としては消えてしまっても、水滴として実体が残っていれば、それは実在するといえるのではないか。当該観察者の目からは消えても、おおかたの観察者にとっては依然として虹に見えているのであり、かつ実体としても存在する。
すなわち、虹は実在する。
実在するものは、客観的な座標系のもとで所在を定めることができる。
山の稜線は実在するか。
理想化されたものとして考えると、稜線には幅がない。質量もない。それでも実在するといえるか。
実在するといえる。稜線は目で見ることができ、現地に行けばその上を歩くことができ、手で触れることもできる。視覚と触覚の両方で認識できるものは、実在するといえる。
適当な座標系があれば(この場合は地図で使われる地理情報になるだろうが)、稜線の座標は決まる。
では、次図の円柱はどうか。

円柱の上面と下面を縁取る円周は実在するか。
この図で円周は実線で描かれているが、現実の円柱には通常そのような線は描かれていない。けれども、円周は円柱の上面と側面を分ける境界として観察者から視認でき、また触れることもできる。すなわち、この円周は山の稜線と本質的に同じものであり、それゆえ実在するといえる。
問題となるのは図の直線部分。
この二本の縦線も円周と同じように実線で描かれているが、これらの線も現実の円柱の一部ではない。
二本の縦線によって示される部位は、円柱と円柱でないもの(円柱の外側)を分ける境目として観察者には見えている。けれども、さわって確かめることはできない。円柱の側面全体に触れることはできても、そこがいま現にわたしの見ている円柱と円柱でないものの境目であるという指標、たとえば突起や溝を、指先で確認できるわけではない。
ただし水平線・地平線と同様、観察者本人を基準とした場合のみ、この縦線の座標を言うことができる。
観察者本人の視野にだけ存在し、触覚で確かめることができない点で、問題の円柱の部位は地平線・水平線の同類である。
これを一般化すると、「輪郭は実在しない」ということが一つの結論として得られる。