地平線、水平線が存在するわけ、およびその所在
地平線、水平線は、具体的などこかに実在するわけではない。
それらは観察者の目の中に仮想的に存在する。
港を船が離れる。
観察者の視界を沖に向かって遠ざかる船体は、やがて下部から少しずつ海面に隠されていき、しばらくは海上に残っていた帆もついに没して全体が視界から消える。
あとには海と空ばかり。
その両者を区切る線を水平線という。
海と空を分ける線が、どうしてそこに見えているのか。具体的、物理的に存在するはずのないものが、なぜそんなところに、存在するかのように見えるのか。
答えは、地球が丸いから。――と自分はずっと思い込んでいた。球体の表面を遠ざかっていくものが、やがて丘のむこうへ越えるようにして視界から消えるのは当然ではないか、と。けれどもこれは勘違い。
自分とおなじ間違いをしている人がどれほどいるかは知らないが、かりに地球が球状ではなく、平板な大地がどこまでも続くのだとしても、やはり地平線、水平線は存在する。もちろんその場合も仮想的な存在ではあるのだが。
地球が平板でも、地平線、水平線が存在するわけは、次のように考えるとわかる。
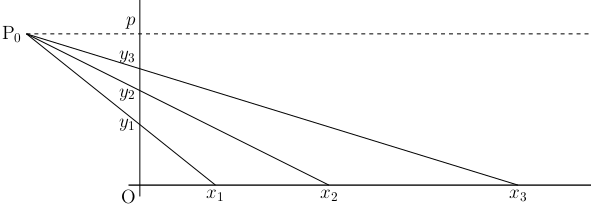
図は山川偉也著『ゼノン 4つの逆理』にあるのとほぼ同じ。オリジナルの図は、パスカルが論文「幾何学的精神について」の一節で述べたことを山川がグラフ化したもの。
遠ざかっていく船を人が透明なガラス板をとおして見ている。
船は原点 O から出発して x 軸上を進む。
O から上方に垂直に伸びる線はガラスの面を表す。パスカルはこれを透明なガラス板としたが、人の網膜とか視野と解するほうが適切か。
P0 は人の目の位置。そこから右へ伸びる点線は船の進む海面と平行な面をあらわし、p はガラス板との接点。
船が x1、x2、x3 と沖へ向かうに連れて、視野における船の位置は y1、y2、y3 と上方へ移動する。
当該部分のテキストでパスカルは、空間が限りなく細かく分割できることを主張した。じっさい、船は x 軸方向へいくらでも進むことができるが、それに対応する y 方向の位置が p を越えることはない。すなわち、[yn, yn+1] などの間隔はいくらでも狭くなり、空間が無限に細かく分割できることが示される。
パスカルの本題から外れるが、P0 と海上の船の位置を結ぶ斜めの線に注目すると、この線はしだいに水平方向に近づくが、けして P0 p を越えることはない。そして、はるか彼方の船が観察者の視野のうちで限りなく P0 p に近づくということは、海と空との境がその方向にあることを意味する。
結論。
地球が丸くなくても、地平線、水平線は存在する。
それらは観察者の目の高さにある。
それらは観察者の目の中に仮想的に存在する。
港を船が離れる。
観察者の視界を沖に向かって遠ざかる船体は、やがて下部から少しずつ海面に隠されていき、しばらくは海上に残っていた帆もついに没して全体が視界から消える。
あとには海と空ばかり。
その両者を区切る線を水平線という。
海と空を分ける線が、どうしてそこに見えているのか。具体的、物理的に存在するはずのないものが、なぜそんなところに、存在するかのように見えるのか。
答えは、地球が丸いから。――と自分はずっと思い込んでいた。球体の表面を遠ざかっていくものが、やがて丘のむこうへ越えるようにして視界から消えるのは当然ではないか、と。けれどもこれは勘違い。
自分とおなじ間違いをしている人がどれほどいるかは知らないが、かりに地球が球状ではなく、平板な大地がどこまでも続くのだとしても、やはり地平線、水平線は存在する。もちろんその場合も仮想的な存在ではあるのだが。
地球が平板でも、地平線、水平線が存在するわけは、次のように考えるとわかる。

図は山川偉也著『ゼノン 4つの逆理』にあるのとほぼ同じ。オリジナルの図は、パスカルが論文「幾何学的精神について」の一節で述べたことを山川がグラフ化したもの。
遠ざかっていく船を人が透明なガラス板をとおして見ている。
船は原点 O から出発して x 軸上を進む。
O から上方に垂直に伸びる線はガラスの面を表す。パスカルはこれを透明なガラス板としたが、人の網膜とか視野と解するほうが適切か。
P0 は人の目の位置。そこから右へ伸びる点線は船の進む海面と平行な面をあらわし、p はガラス板との接点。
船が x1、x2、x3 と沖へ向かうに連れて、視野における船の位置は y1、y2、y3 と上方へ移動する。
当該部分のテキストでパスカルは、空間が限りなく細かく分割できることを主張した。じっさい、船は x 軸方向へいくらでも進むことができるが、それに対応する y 方向の位置が p を越えることはない。すなわち、[yn, yn+1] などの間隔はいくらでも狭くなり、空間が無限に細かく分割できることが示される。
パスカルの本題から外れるが、P0 と海上の船の位置を結ぶ斜めの線に注目すると、この線はしだいに水平方向に近づくが、けして P0 p を越えることはない。そして、はるか彼方の船が観察者の視野のうちで限りなく P0 p に近づくということは、海と空との境がその方向にあることを意味する。
結論。
地球が丸くなくても、地平線、水平線は存在する。
それらは観察者の目の高さにある。