「竹取物語」で読む月までの距離
帝への手紙と不死の薬を残して、かぐや姫は月の世界に帰ってしまう。
手紙と薬を受け取った帝が、近臣を召して、
「どの山が天に近いか」
とたずねると、ひとりが、
「駿河にある山が都にも近く天にも近い」
と奏上したので、帝は駿河に使いを派遣し、その山の頂上で手紙と不死の薬を焼かせた。
その後この山は「富士の山」と命名された。
これが「竹取物語」のエンディング。
「竹取」の作者や受容層が地上から月までの距離をどの程度と見ていたか、この末尾の出来事から推量できる。
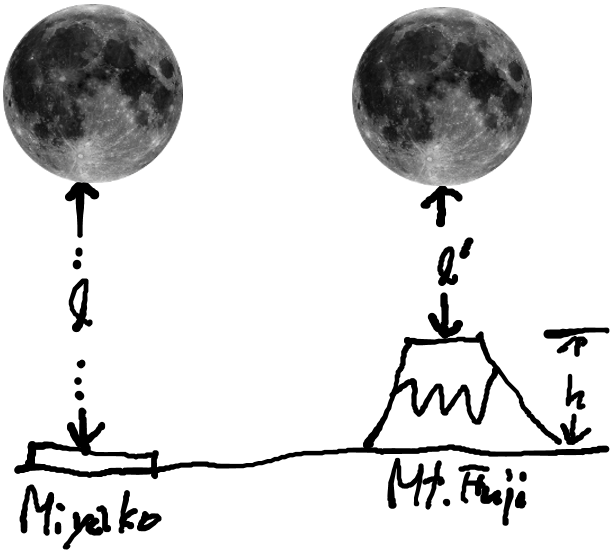
月が中天に達したときの都と月の距離を l とする。
同様に富士山頂と月の距離を l' とする。
また富士山の高さを h とすると、これらの関係は l = l' + h となる。
竹取物語は帝の内面を描いていないが、何らかのメッセージを煙に託そうとしたのはまちがいなく、都で手紙を焼くより富士山で焼くほうが月の世界からずっとはっきり煙を視認できると期待したからには、l' を l に比べて相当程度小さく見込んだはずである。
では帝は、というより物語の作者や受容層はということだが、l' をどの程度小さく見込んだか。l より1割か2割短いというのでは、はるばる使者をつかわす甲斐はない。少なくとも、半分(l' = l/2)、あるいは3分の1ほど(l' = l/3)に縮まるのでなければ意味はないから、その前提で l と h の比を計算すると、
半分ならば、l = 2h
3分の1ならば、l = 1.5h
となり、現在知られている富士山の高さ(約4km)を h に代入すると、地上から月への距離は 6〜8km となる。
この 6〜8km という値は生物学者・哲学者のユクスキュルが伝える人間の最遠平面の半径にぴったり一致する。
参考: 天球の半径
数値の設定(l' = l/2 または l' = l/3)がうまくはまった幸運な一致だが、月と地球の現実の距離(約40万km)とのオーダーの違い(10万倍)があるから、この幸運は数学的にも許容範囲。「竹取物語」の成立時期とされる平安初期の人々も現代のわれわれと同じスケールで天空を見ていたのである。
手紙と薬を受け取った帝が、近臣を召して、
「どの山が天に近いか」
とたずねると、ひとりが、
「駿河にある山が都にも近く天にも近い」
と奏上したので、帝は駿河に使いを派遣し、その山の頂上で手紙と不死の薬を焼かせた。
その後この山は「富士の山」と命名された。
これが「竹取物語」のエンディング。
「竹取」の作者や受容層が地上から月までの距離をどの程度と見ていたか、この末尾の出来事から推量できる。

月が中天に達したときの都と月の距離を l とする。
同様に富士山頂と月の距離を l' とする。
また富士山の高さを h とすると、これらの関係は l = l' + h となる。
竹取物語は帝の内面を描いていないが、何らかのメッセージを煙に託そうとしたのはまちがいなく、都で手紙を焼くより富士山で焼くほうが月の世界からずっとはっきり煙を視認できると期待したからには、l' を l に比べて相当程度小さく見込んだはずである。
では帝は、というより物語の作者や受容層はということだが、l' をどの程度小さく見込んだか。l より1割か2割短いというのでは、はるばる使者をつかわす甲斐はない。少なくとも、半分(l' = l/2)、あるいは3分の1ほど(l' = l/3)に縮まるのでなければ意味はないから、その前提で l と h の比を計算すると、
半分ならば、l = 2h
3分の1ならば、l = 1.5h
となり、現在知られている富士山の高さ(約4km)を h に代入すると、地上から月への距離は 6〜8km となる。
この 6〜8km という値は生物学者・哲学者のユクスキュルが伝える人間の最遠平面の半径にぴったり一致する。
参考: 天球の半径
数値の設定(l' = l/2 または l' = l/3)がうまくはまった幸運な一致だが、月と地球の現実の距離(約40万km)とのオーダーの違い(10万倍)があるから、この幸運は数学的にも許容範囲。「竹取物語」の成立時期とされる平安初期の人々も現代のわれわれと同じスケールで天空を見ていたのである。